Understanding reticular patterns
Leaf vein network
Pattern on the wing of a dragonfly
Fractures on the surface of ceramics
Two-dimensional foam
Many spatial patterns have a "reticular" or networklike form: leaf veins, lines of fracture in the glaze of ceramics, the pattern on the wings of dragonflies are just a few examples.
Scientists often produce theoretical models or computer simulations to understand how these different patterns are generated and grow over time. Such models are very difficult to validate or falsify unless we are able to quantify how good results they produce, how similar the real pattern is to the simulated one.
This is why we need to produce simple but meaningful quantitative descriptions of the patterns.
Topology of reticular patterns
One possibility is to describe these patterns in terms of graphs. Each junction can be mapped into a node and the segments of linear structure are mapped into edges. We can then compute a number of network parameters to describe the pattern. If the estimators are meaningful, they will give different numbers for patterns that we intuitively see as different.
Unfortunately, the topology of these graphs does not give much information. Almost all these patterns are planar, which means that their total number of edges E, vertices V and faces F is constrained by Euler's formula, which imposes that
V-E+F=2
from which follows for instance that the average degree cannot be higher than six.
In addition, almost all the vertices in such diverse networks as fracture lines, bidimensional foams and leaf veins have degree equal to three.
These and other constraints make it difficult to characterise reticular patterns only based on their topology.
The importance of geometry
The geometry of the lines that meet at junctions carries a lot of information on the characteristics of the pattern and its history of growth.
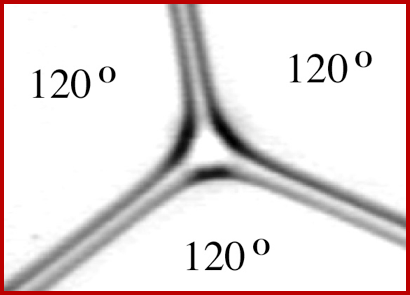
A common morphology is one where segments at junctions form three equal angles of 120 degrees. This configuration occurs in two-dimensional foams, honeycombs, in the arrangement of cell membranes in biological epithelia, but also in geological formations such as columnar joints found in basaltic lava rocks (such as the Giant's Causeway). We can think to these symmetric, tripartite junctions as to the result of forces directed to minimize the local length of network segments around the junction.
Another common configuration involves orthogonal junctions of 180 and 90 degrees. This configuration is typical of patterns that grow in time without undergoing significant reorganization, such as ceramics fractures, street patterns in unplanned cities, leaf veins. In these patterns, the "old" segment continues in a more or less straight direction across the junction (because it was formed before the junction itself), while the new one forms a large angle of about 90 degrees with the other two.
So, the history of growth of the pattern is partially written in its final configuration and we can try to reconstruct it by looking at the final pattern.
Together with Stéphane Douady and Pascale Kuntz I have been working at methods for mapping the information about geometry onto a graph representation.
Related scientific publications
- Perna et al. "Characterization of spatial networklike patterns from junction geometry". Physical Review E (2011) [Pdf] [Web]